
আমরা এই অধ্যায়ে (S N De Maths , Chhaya Publisher) বিন্যাস সংক্রান্ত দীর্ঘ উত্তর ধর্মী প্রশ্নোত্তর [Ex- 7A, Long Ans Type : Qst No. 1-5] আলোচনা করব ।
1. n সংখ্যক বিভিন্ন বস্তু থেকে একযোগে ![]() সংখ্যক বস্তুর বিন্যাস সংখ্যা
সংখ্যক বস্তুর বিন্যাস সংখ্যা ![]() হলে দেখাও যে,
হলে দেখাও যে,
![]()
Solution.
আমরা জানি,
![]()
স্পষ্টতই ![]() নং সম্পর্কটি একটি অভেদ(identity).
নং সম্পর্কটি একটি অভেদ(identity).
এখন, ![]() বসিয়ে পাই,
বসিয়ে পাই,

যোগ করে পাই,
![]()
2. যদি ![]() হয়, দেখাও যে,
হয়, দেখাও যে, ![]()
Solution.

একই ভাবে,

(1) ও (2) থেকে পাই,
![]()
3. প্রমাণ করো যে ![]() সংখ্যক জিনিসের সবগুলি একত্রে নিয়ে বিন্যাস সংখ্যার যত গুলিতে নির্দিষ্ট
সংখ্যক জিনিসের সবগুলি একত্রে নিয়ে বিন্যাস সংখ্যার যত গুলিতে নির্দিষ্ট ![]() সংখ্যক বস্তু কখনো পাশাপাশি না থাকে তার সংখ্যা হয়
সংখ্যক বস্তু কখনো পাশাপাশি না থাকে তার সংখ্যা হয় ![]()
Solution.
n সংখ্যক জিনিসের সবগুলি কে একত্রে নিয়ে এমনভাবে বিন্যাস করতে হবে যাতে নির্দিষ্ট m সংখ্যক জিনিস কখনো পাশাপাশি থাকবে না। কোনো বাধ্যবাধকতা না থাকলে বা কোন শর্ত আরোপিত না থাকলে n সংখ্যক নির্দিষ্ট জিনিসকে ![]() প্রকারে বিন্যস্ত করা সম্ভব। সুতরাং m সংখ্যক নির্দিষ্ট জিনিসকে একটি জিনিস ধরলে জিনিসের সংখ্যা হয়
প্রকারে বিন্যস্ত করা সম্ভব। সুতরাং m সংখ্যক নির্দিষ্ট জিনিসকে একটি জিনিস ধরলে জিনিসের সংখ্যা হয় ![]() এই সংখ্যক জিনিসগুলোকে নিজেদের মধ্যে
এই সংখ্যক জিনিসগুলোকে নিজেদের মধ্যে ![]() প্রকারে বিন্যস্ত করা যাবে। আবার
প্রকারে বিন্যস্ত করা যাবে। আবার ![]() সংখ্যক নির্দিষ্ট জিনিসকে নিজেদের মধ্যে
সংখ্যক নির্দিষ্ট জিনিসকে নিজেদের মধ্যে ![]() প্রকারে বিন্যস্ত করা
প্রকারে বিন্যস্ত করা
যাবে। সুতরাং যে বিন্যাসগুলোতে নির্দিষ্ট ![]() সংখ্যক জিনিস পাশাপাশি থাকবে তাদের সংখ্যা হল
সংখ্যক জিনিস পাশাপাশি থাকবে তাদের সংখ্যা হল ![]()
কাজেই যে বিন্যাস গুলিতে m সংখ্যক নির্দিষ্ট জিনিস পাশাপাশি থাকবে না তার সংখ্যা হল ![]()
4. একই অংক একাধিকবার ব্যবহার না করে ![]() এই অংকগুলোর সাহায্যে
এই অংকগুলোর সাহায্যে ![]() অপেক্ষা ছোট এবং
অপেক্ষা ছোট এবং ![]() দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা নির্ণয় করো।
দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা নির্ণয় করো।
Sol. স্পষ্টতই ![]() অপেক্ষা ক্ষুদ্রতর সংখ্যা (i) 1 অংকবিশিষ্ট (ii) 2 অংকবিশিষ্ট অথবা (iii) 3 অংক বিশিষ্ট হতে পারে।
অপেক্ষা ক্ষুদ্রতর সংখ্যা (i) 1 অংকবিশিষ্ট (ii) 2 অংকবিশিষ্ট অথবা (iii) 3 অংক বিশিষ্ট হতে পারে।
(i) এখন এক অংক বিশিষ্ট সংখ্যা হতে পারে, কারণ ছটি অংক প্রদত্ত। প্রদত্ত 6 টি অংকের মধ্যে তিনটি অঙ্ক ![]() দ্বারা বিভাজ্য।
দ্বারা বিভাজ্য।
(ii) 2 দ্বারা বিভাজ্য দুই অংক বিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে অতি অবশ্যই ![]() অথবা
অথবা ![]() কে বসাতে হবে।
কে বসাতে হবে।
2 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
অনুরুপে 4 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
এবং 6 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
অতএব 2 দ্বারা বিভাজ্য দুই অংক বিশিষ্ট সংখ্যার সংখ্যা
![]()
![]() দ্বারা বিভাজ্য
দ্বারা বিভাজ্য ![]() অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে অতি অবশ্যই
অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে অতি অবশ্যই ![]() অথবা
অথবা ![]() কে বসাতে হবে।
কে বসাতে হবে। ![]() দ্বারা বিভাজ্য
দ্বারা বিভাজ্য ![]() অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে
অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে ![]() কে বসালে বাকি পাঁচটি অঙ্ককে দুটি স্থানে
কে বসালে বাকি পাঁচটি অঙ্ককে দুটি স্থানে ![]() প্রকারে সাজানো যায়।
প্রকারে সাজানো যায়।
2 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
অনুরুপে 4 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
এবং 6 কে একক স্থানে বসালে গঠিত সংখ্যার সংখ্যা=![]()
সুতরাং 2 দ্বারা বিভাজ্য 3 অঙ্ক বিশিষ্ট সংখ্যার সংখ্যা
![]()
একই অংক একাধিকবার ব্যবহার না করে ![]() এই অংকগুলোর সাহায্যে
এই অংকগুলোর সাহায্যে ![]() অপেক্ষা ছোট এবং
অপেক্ষা ছোট এবং ![]() দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা=
দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা= ![]()
5. 0,1,2,3,4,5,6,7,8,9 অংকগুলির সাহায্যে ![]() অপেক্ষা ছোট এবং
অপেক্ষা ছোট এবং ![]() দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা নির্ণয় করো, কোন সংখ্যায় কোন অংক একবারের বেশি থাকবে না?
দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা নির্ণয় করো, কোন সংখ্যায় কোন অংক একবারের বেশি থাকবে না?
Sol. স্পষ্টতই ![]() অপেক্ষা ক্ষুদ্রতর সংখ্যা
অপেক্ষা ক্ষুদ্রতর সংখ্যা ![]() অঙ্কবিশিষ্ট
অঙ্কবিশিষ্ট ![]() অঙ্কবিশিষ্ট অথবা
অঙ্কবিশিষ্ট অথবা ![]() অংক বিশিষ্ট হতে পারে।
অংক বিশিষ্ট হতে পারে।
(i) 1 অঙ্কবিশিষ্ট 5 দ্বারা বিভাজ্য সংখ্যার সংখ্যা হবে একটি। যথাঃ 5.
(ii) 5 দ্বারা বিভাজ্য দুই অংক বিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একই স্থানে অতি অবশ্যই ![]() কিংবা
কিংবা ![]() কে বসাতে হবে।
কে বসাতে হবে।
দুই অংক বিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে 5 রাখলে গঠিত সংখ্যার সংখ্যা হবে=![]() টি কেননা এক্ষেত্রে দশকের স্থানে শূন্য থাকার ক্ষেত্রটি বাদ দিতে হবে।
টি কেননা এক্ষেত্রে দশকের স্থানে শূন্য থাকার ক্ষেত্রটি বাদ দিতে হবে।
আবার একক খানে শূন্যকে রাখলে গঠিত সংখ্যার সংখ্যা হবে= ![]() টি ।
টি ।
এতদিন সুতরাং ![]() দ্বারা বিভাজ্য দুই অংক বিশিষ্ট সংখ্যার সংখ্যা হবে=
দ্বারা বিভাজ্য দুই অংক বিশিষ্ট সংখ্যার সংখ্যা হবে=
![]()
(iii) ![]() দ্বারা বিভাজ্য
দ্বারা বিভাজ্য ![]() অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে অতি অবশ্যই
অংকবিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে অতি অবশ্যই ![]() কিংবা
কিংবা ![]() কে রাখতে হবে।
কে রাখতে হবে। ![]() অংক বিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে
অংক বিশিষ্ট সংখ্যা গঠনের ক্ষেত্রে একক স্থানে ![]() কে রাখলে গঠিত সংখ্যার সংখ্যা=
কে রাখলে গঠিত সংখ্যার সংখ্যা= ![]() কেননা এক্ষেত্রে শতকের স্থানে শূন্য আসার ক্ষেত্রগুলো বাদ দিতে হয়।
কেননা এক্ষেত্রে শতকের স্থানে শূন্য আসার ক্ষেত্রগুলো বাদ দিতে হয়।
আবার একক স্থানে শূন্য বসালে গঠিত সংখ্যার সংখ্যা=![]()
সুতরাং ![]() দ্বারা বিভাজ্য
দ্বারা বিভাজ্য ![]() অংকবিশিষ্ট সংখ্যার সংখ্যা= 5 দ্বারা বিভাজ্য হাজার অপেক্ষা ক্ষুদ্রতর সংখ্যার সংখ্যা
অংকবিশিষ্ট সংখ্যার সংখ্যা= 5 দ্বারা বিভাজ্য হাজার অপেক্ষা ক্ষুদ্রতর সংখ্যার সংখ্যা
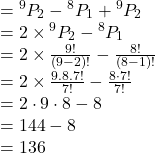
সুতরাং ![]() অংকগুলির সাহায্যে
অংকগুলির সাহায্যে ![]() অপেক্ষা ছোট এবং
অপেক্ষা ছোট এবং ![]() দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা
দ্বারা বিভাজ্য যতগুলো সংখ্যা গঠন করা যায় তার সংখ্যা ![]()