টি বিভিন্ন ব্যঞ্জনবর্ণ থেকে দুটি ব্যঞ্জন বর্ণ এবং পাঁচটি স্বরবর্ণ থেকে তিনটি স্বরবর্ণ একযোগে নিয়ে পাঁচটি অক্ষর বিশিষ্ট কতগুলি বিভিন্ন শব্দ গঠন করা যায়?
Solution.
টি বিভিন্ন ব্যঞ্জনবর্ণ থেকে দুটি ব্যঞ্জনবর্ণ 
প্রকারে নির্বাচন করা যায়। আবার পাঁচটি স্বরবর্ণ থেকে তিনটি স্বরবর্ণ 
প্রকারে নির্বাচন করা যায়।
আবার দুটি ব্যঞ্জন বর্ণ এবং তিনটি স্বরবর্ণ মিলে পাঁচটি অক্ষর নিজেদের মধ্যে 
প্রকারে বিন্যস্ত হতে পারে।
সুতরাং এক্ষেত্রে এক্ষেত্রে নির্ণেয় মোট নির্বাচন সংখ্যা হল
টি বিভিন্ন ব্যঞ্জনবর্ণ এবং 
টি বিভিন্ন স্বরবর্ণ থেকে 
টি ব্যঞ্জন বর্ণ ও 
টি স্বরবর্ণ নিয়ে কতগুলি বিভিন্ন শব্দ গঠন করা যায়?
Solution.
টি বিভিন্ন ব্যঞ্জনবর্ণ থেকে টি ব্যঞ্জনবর্ণ 
প্রকারে নির্বাচন করা যায়। আবার টি স্বরবর্ণ থেকে টি স্বরবর্ণ প্রকারে নির্বাচন করা যায়।
আবার 
টি ব্যঞ্জন বর্ণ এবং 
টি স্বরবর্ণ মিলে টি অক্ষর নিজেদের মধ্যে 
প্রকারে বিন্যস্ত হতে পারে।
সুতরাং এক্ষেত্রে এক্ষেত্রে নির্ণেয় মোট নির্বাচন সংখ্যা হল
11. এক ব্যক্তির 
জন পরিচিত ব্যক্তি আছেন এবং তাদের মধ্যে 
জন তার আত্মীয় । কত বিভিন্ন উপায়ে তিনি জনকে অতিথি হিসাবে আহবান করতে পারবেন যাতে নিমন্ত্রিত ব্যক্তিদের মধ্যে 
জন আত্মীয় হবেন?
Solution.
প্রশ্ন অনুযায়ী, জন পরিচিত ব্যক্তির মধ্যে জন আত্মীয় হলে , আত্মীয় নয় এমন লোকের সংখ্যা 
জন। কে অতিথি হিসেবে এমনভাবে আহবান করতে হবে যাতে জন আত্মীয় হয়। এই সাত জনকে তাহলে জন আত্মীয়ের মধ্যে নিতে হবে যেটি সম্ভব =
প্রকারে।
সেক্ষেত্রে বাকি দু’জনকে 
আত্মীয় নয় এমন লোকের মধ্য থেকে নির্বাচিত করতে হবে যেটি সম্ভব=
প্রকারে। সুতরাং এক্ষেত্রে মোট নির্বাচনের সংখ্যা হল
জন লোকের মধ্য থেকে কত বিভিন্ন উপায়ে জন লোক নির্বাচন করা যায় যাতে (i) নির্দিষ্ট তিনজন লোক সর্বদা বাদ পড়ে (ii) নির্দিষ্ট জন লোক সর্বদা থাকবে ?
Solution.
1st part : জনের মধ্যে জন নির্দিষ্ট লোককে বাদ দিতে হলে অবশিষ্ট লোকের সংখ্যা হয় 
জন। এই জন লোকের মধ্যে জনকে নির্বাচিত করা যেতে পারে=
প্রকারে।
2nd part: জন নির্দিষ্ট লোককে সর্বদা রাখতে হলে অবশিষ্ট জন লোকের মধ্যে 
জনকে নির্বাচিত করা যায় =
প্রকারে।
জন ভদ্রমহিলা ও 
জন ভদ্রলোকের মধ্য থেকে কত রকমে 
জন ভদ্রমহিলা ও 
জন ভদ্রলোকের কমিটি গঠন করা যায় ? শ্রীযুক্ত 
যদি একজন সদস্য হন তবে শ্রীমতি 
কমিটিতে থাকতে অস্বীকৃত হন এমন কতগুলি ক্ষেত্র হতে পারে?
Solution.
1st part: 
জন ভদ্রমহিলার মধ্য থেকে জন ভদ্রমহিলা নির্বাচিত করা যেতে পারে 
প্রকারে । একইভাবে সাত জন ভদ্রলোকের মধ্য থেকে চার জন ভদ্রলোকের নির্বাচন করা যায় 
প্রকারে ।
সুতরাং এক্ষেত্রে এক্ষেত্রে নির্ণেয় মোট নির্বাচন সংখ্যা হল=
2nd part: প্রথমত, শ্রীযুক্ত যদি একজন সদস্য হন তবে শ্রীমতি কমিটিতে থাকতে অস্বীকৃত হন। এইরূপ ক্ষেত্র হতে পারে=
প্রকারে।
একইভাবে, শ্রীযুক্ত যদি একজন সদস্য না হন তবে শ্রীমতি কমিটিতে থাকতে স্বীকৃত হন। এইরূপ ক্ষেত্র হতে পারে=
প্রকারে।
ও 
থেকে পাই, মোট নির্বাচন সংখ্যা =
13(ii) যাতে কোনো দুজন স্ত্রীলোক পাশাপাশি না থাকে এভাবে 
জন পুরুষ এবং 
জন স্ত্রীলোক এক সারিতে আসন গ্রহণ করে। যদি 
হয়, তবে দেখাও যে, তারা 
প্রকারে আসন গ্রহন করতে পারে ?
Solution.
যদি কোন স্ত্রীলোক পাশাপাশি না থাকে তবে জন পুরুষকে 
এই সংখ্যক স্থানে থাকতে হবে এবং জন স্ত্রীলোককে জন পুরুষের মধ্যবর্তী স্থানে এবং দুই প্রান্তে অর্থাৎ 
টি স্থানে থাকতে হবে ।
এখন, সংখ্যক পুরুষ সংখ্যক স্থানে থাকতে পারে 
রকমে, আবার সংখ্যক স্ত্রীলোক 
সংখ্যক স্থানে থাকতে পারে 
রকমে ।
সুতরাং কোন দুজন স্ত্রীলোক পাশাপাশি না রেখে বিন্যাসের সংখ্যা হল
কোনো লটারিতে 
টি পুরস্কার ঘোষণা করা হয়। প্রথম অংশগ্রহণকারী 
টি টিকিটের একটি বাক্স থেকে টি টিকিট তোলে। কত বিভিন্ন উপায়ে টিকিট টি তুললে সে ঠিক দুটি পুরস্কারজয়ী টিকিট তুলবে?
Solution.
8 টি পুরস্কারের টিকিটের মধ্যে দুটি পুরস্কারের টিকিট নির্বাচন করা যায় 
রকমে । আবার অবশিষ্ট তিনটি পুরস্কার ছাড়া টিকিট নির্বাচন করা করতে হবে 
টি টিকিটের মধ্য থেকে, যা 
রকমে সম্ভব।
সুতরাং সে ঠিক দুটি পুরস্কারজয়ী তুলবে 
রকমে ।
জন নির্বাচন প্রার্থীর মধ্য থেকে জন সদস্য নির্বাচন করতে হবে। একজন ভোটদাতা যতজন নির্বাচিত হবেন তার অনধিক যতজন প্রার্থীকে ইচ্ছা ভোট দিতে পারেন। তিনি কত বিভিন্ন উপায়ে ভোট দিতে পারেন?
Sol. একজন ভোটদাতা,
1 জন প্রার্থীকে ভোট দিতে পারেন 
রকমে,
2 জন প্রার্থীকে ভোট দিতে পারেন 
রকমে,
3 জন প্রার্থীকে ভোট দিতে পারেন 
রকমে,
4 জন প্রার্থীকে ভোট দিতে পারেন 
রকমে ।
সুতরাং একজন ভোটদাতা অনধিক জন প্রার্থীকে ভোট দিতে পারেন
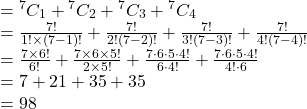
রকমে ।