![]() এর মধ্যে কত বিভিন্ন রকম উৎপাদক আছে?
এর মধ্যে কত বিভিন্ন রকম উৎপাদক আছে?
Solution.
আমরা জানি, ![]() সংখ্যক বিভিন্ন বস্তু থেকে একযোগে যতগুলো ইচ্ছা বস্তু নিয়ে সমবায় সংখ্যা হল
সংখ্যক বিভিন্ন বস্তু থেকে একযোগে যতগুলো ইচ্ছা বস্তু নিয়ে সমবায় সংখ্যা হল ![]()
এখানে, ![]() , যেহেতু
, যেহেতু ![]() টি বিভিন্ন উৎপাদক আছে । কারন,
টি বিভিন্ন উৎপাদক আছে । কারন, ![]()
সুতরাং, এক্ষেত্রে ![]() থেকে পাই,
থেকে পাই, ![]() এর মধ্যে
এর মধ্যে ![]() টি বিভিন্ন রকম উৎপাদক আছে।
টি বিভিন্ন রকম উৎপাদক আছে।
![]() কোন পরীক্ষায় পাস করতে হলে একজন পরীক্ষার্থীকে
কোন পরীক্ষায় পাস করতে হলে একজন পরীক্ষার্থীকে ![]() টি বিষয়ের প্রত্যেকটিতে একটি ন্যূনতম নম্বর পেতে হয়। কত উপায়ে একজন পরীক্ষার্থী পরীক্ষায় ফেল করতে পারে?
টি বিষয়ের প্রত্যেকটিতে একটি ন্যূনতম নম্বর পেতে হয়। কত উপায়ে একজন পরীক্ষার্থী পরীক্ষায় ফেল করতে পারে?
Solution.
ধরা যাক, পরীক্ষার্থীটি একটি বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে।
প্রকারে।
একই ভাবে, পরীক্ষার্থীটি ![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে,![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে,![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে, ![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে,![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে, ![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে,
প্রকারে,![]() বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব
বিষয়ে ন্যূনতম নম্বর না পেয়ে ফেল করতে পারে এবং এটি সম্ভব ![]() প্রকারে।
প্রকারে।
সুতরাং, এক্ষেত্রে মোট নির্বাচন সংখ্যা


![]() হলে,
হলে, ![]()
Solution.
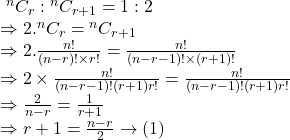
![Rendered by QuickLaTeX.com \,\,{}^{n}C_{r+1} : {}^{n}C_{r+2}=2:3 \\ \Rightarrow 3. {}^{n}C_{r+1}=2.{}^{n}C_{r+2} \\ \Rightarrow 2.\frac{n!}{(n-r-1)!\times (r+1)!}\\= \frac{n!}{(n-r-2)! \times (r+2)!} \\ \Rightarrow \frac{2}{(n-r-1)(n-r-2)! \times (r+1)!}\\=\frac{1}{(n-r-2)! \times (r+2)(r+1)!} \\ \Rightarrow r+2=\frac23 \times (n-r-1) \\ \Rightarrow (r+1)+1= \frac23 \times (n-r-1) \\ \Rightarrow \frac{n-r}{2}+1= \frac23 \times (n-r-1) \\ \Rightarrow 6\left(\frac{n-r}{2}+1\right)= 6\left[\frac23 \times (n-r-1)\right] \\ \Rightarrow 3(n-r)+6=4(n-r-1)\\ \Rightarrow n-r=10 \rightarrow (2)](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-7b18c3ae3d88bcf88af37d040f450643_l3.png)
এখন, ![]() ও
ও ![]() থেকে পাই,
থেকে পাই,
![]()
আবার, ![]() থেকে পাই,
থেকে পাই,
![]()
![]() ও
ও ![]() হলে,
হলে, ![]() ও
ও ![]() -এর মান নির্ণয় কর।
-এর মান নির্ণয় কর।
Solution.

![]() হলে, দেখাও যে,
হলে, দেখাও যে, ![]()
Solution.
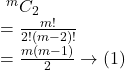
কিন্তু, ![]()
![]() ও
ও ![]() হতে পাই,
হতে পাই,
![Rendered by QuickLaTeX.com {}^{m}C_2\\=\frac12 . \frac{n(n-1)}{2}. \left[\frac{n(n-1)}{2}-1\right] \\=\frac18. n(n-1)(n^2-n-2) \rightarrow (3)](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-4ceebd814333a4ca15aceebfc0d593d1_l3.png)
![Rendered by QuickLaTeX.com \text{আবার,}\, 3 \times {}^{n+1}C_4\\ =3. \frac{(n+1)!}{4!\times (n+1-4)}\\= \frac{3}{4\cdot 3 \cdot 2\cdot 1} \times \frac{(n+1)n(n-1)(n-2)(n-3)!}{(n-3)!}\\=\frac18 \times n(n-1) \left[(n+1)(n-2) \right]\\= \frac18 n(n-1)(n^2-n-2) \rightarrow (4)](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-97970b57439dd6cf8613d2ca309794e0_l3.png)
![]() ও
ও ![]() থেকে পাই,
থেকে পাই,
![]()
![]() ও
ও ![]() হলে,
হলে, ![]() ও
ও ![]() এর মান নির্ণয় কর ।
এর মান নির্ণয় কর ।
Solution.


![]() ও
ও ![]() হতে পাই,
হতে পাই,

আবার, ![]() হতে পাই,
হতে পাই,
![]()
![]() প্রমাণ করঃ
প্রমাণ করঃ
![]()
Solution.
![]()
![]()

![]()
Solution. Check S.N.De workout example
![]()
Solution.

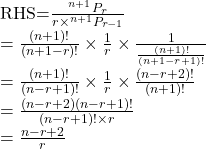
সুতরাং, LHS=RHS (proved)
![]()
Solution.
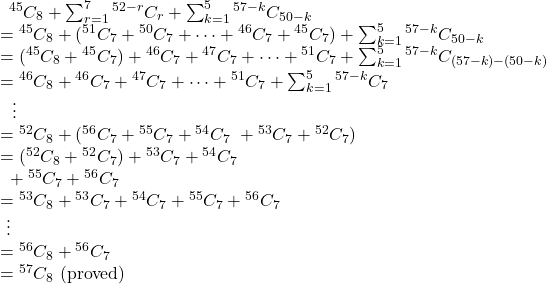
![]()
Solution.
![Rendered by QuickLaTeX.com \,\,{}^{15}C_8+{}^{15}C_9-{}^{15}C_6-{}^{15}C_7\\=[{}^{15}C_8+{}^{15}C_9]-[{}^{15}C_6+{}^{15}C_7]\\={}^{15+1}C_9-{}^{15+1}C_7\\~~~~~~~~~[\because {}^nC_r+ {}^nC_{r-1}={}^{n+1}C_r]\\={}^{16}C_9-{}^{16}C_7\\=\frac{16}{9!\times (16-9)!}-\frac{16}{7!\times (16-7)!}\\=\frac{16!}{9!7!}-\frac{16!}{7!9!}\\=0\,\,\,\text{(proved)}](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-256c20217a4a4c8df768605b0f185ef2_l3.png)