
![]() রাশির অবম মান হবে-
রাশির অবম মান হবে-
![]()
Solution.

![]() correct.
correct.
![]() রাশির চরম মান হবে-
রাশির চরম মান হবে-
![]()
Solution.
![Rendered by QuickLaTeX.com \,\,4x-x^2-2\\=-(x^2-4x+2)\\=-[x^2-2\times x\times 2+2^2-2]\\=-(x-2)^2+2 \rightarrow(1)](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-e095ab1d3a7961228dfdab23849c86b7_l3.png)
এখন, 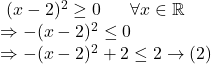
সুতরাং, ![]() ও
ও ![]() থেকে বলা যায়,
থেকে বলা যায়, ![]() option টি সঠিক।
option টি সঠিক।
![]() সমীকরণের একটি বীজ
সমীকরণের একটি বীজ ![]() হলে, নিচের কে সমীকরণটির অন্য বীজ হবে ?
হলে, নিচের কে সমীকরণটির অন্য বীজ হবে ?
![]()
Solution.
![]() সমীকরণের একটি বীজ
সমীকরণের একটি বীজ ![]() ,
,
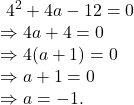
সুতরাং, সমীকরণ টি হল,

![]() correct.
correct.
![]() সমীকরণের বীজ দুটির যোগফল নীচের কোন মানটির সমান বলো?
সমীকরণের বীজ দুটির যোগফল নীচের কোন মানটির সমান বলো?
![]()
Solution.
![]() দ্বিঘাত সমীকরণের বীজদ্বয়
দ্বিঘাত সমীকরণের বীজদ্বয় ![]() হলে
হলে
![]() বীজদ্বয়ের যোগফল
বীজদ্বয়ের যোগফল ![]() ও
ও
![]() বীজদ্বয়ের গুণফল
বীজদ্বয়ের গুণফল ![]()
সুতরাং, ![]() সমীকরণের বীজ দুটির যোগফল
সমীকরণের বীজ দুটির যোগফল
![]() correct.
correct.
![]() নীচের কোন্ মানটি
নীচের কোন্ মানটি ![]() সমীকরণের বীজ দুটি গুণফলের সমান ?
সমীকরণের বীজ দুটি গুণফলের সমান ?
![]()
Solution.
![]() সমীকরণের বীজ দুটি গুণফল
সমীকরণের বীজ দুটি গুণফল
![]() correct.
correct.
Note : ![]() দ্বিঘাত সমীকরণের বীজদ্বয়
দ্বিঘাত সমীকরণের বীজদ্বয় ![]() হলে
হলে
![]() বীজদ্বয়ের যোগফল
বীজদ্বয়ের যোগফল ![]() ও
ও
![]() বীজদ্বয়ের গুণফল
বীজদ্বয়ের গুণফল ![]()
![]() ও
ও ![]() নীচের কোন্ সমীকরণের দুটি বীজ বলো ?
নীচের কোন্ সমীকরণের দুটি বীজ বলো ?
![]()
Solution.
![]() একটি দ্বিঘাত সমীকরণের বীজদ্বয়
একটি দ্বিঘাত সমীকরণের বীজদ্বয় ![]() হলে দ্বিঘাত সমীকরণটি হবে
হলে দ্বিঘাত সমীকরণটি হবে
![]() (বীজদ্বয়ের যোগফল)
(বীজদ্বয়ের যোগফল)![]() বীজদ্বয়ের গুণফল
বীজদ্বয়ের গুণফল ![]()
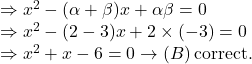
![]() সমীকরণের বীজ দুটি পরস্পর অন্যোন্যক নীচের কোনটি
সমীকরণের বীজ দুটি পরস্পর অন্যোন্যক নীচের কোনটি ![]() -এর মান হবে ?
-এর মান হবে ?
![]()
Solution.
![]() সমীকরণের বীজ দুটি পরস্পর অন্যোন্যক হলে ধরি, বীজ দুটি
সমীকরণের বীজ দুটি পরস্পর অন্যোন্যক হলে ধরি, বীজ দুটি ![]() .
.
![]() বীজদ্বয়ের গুণফল
বীজদ্বয়ের গুণফল ![]()
![]()
![]() সমীকরণের বীজ দুটির যোগফল
সমীকরণের বীজ দুটির যোগফল ![]() হলে নিচের কোনটি
হলে নিচের কোনটি ![]() -এর মান হবে ?
-এর মান হবে ?
![]()
Sol. ![]() সমীকরণের বীজ দুটির
সমীকরণের বীজ দুটির ![]() যোগফল
যোগফল ![]() হলে,
হলে,

![]() সমীকরণের বীজ দুটির গুণফল
সমীকরণের বীজ দুটির গুণফল ![]() হলে নিচের কোনটি
হলে নিচের কোনটি ![]() মান হবে ?
মান হবে ?
![]()
Solution.
![]() সমীকরণের বীজ দুটির
সমীকরণের বীজ দুটির ![]() গুণফল
গুণফল ![]() হলে ,
হলে ,
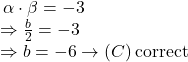
![]() সমীকরণের বীজ দুটি সমান হলে নিচের কোনটি
সমীকরণের বীজ দুটি সমান হলে নিচের কোনটি ![]() এর মান হবে?
এর মান হবে?
![]()
Solution.
![]() সমীকরণের বীজ দুটি
সমীকরণের বীজ দুটি![]() সমান হলে,
সমান হলে,
![Rendered by QuickLaTeX.com \alpha+\beta=-\frac{(-5)}{3} \\ \Rightarrow 2\alpha=\frac 53~~~[\because \alpha=\beta] \\ \Rightarrow \alpha=\frac{5}{6} \\ \Rightarrow \alpha^2=\frac{25}{36} \\ \Rightarrow \alpha \times \alpha=\frac{25}{36} \\ \Rightarrow \frac p3=\frac{25}{36} \\ \Rightarrow p=\frac{25}{12} \rightarrow (B)\,\text{correct}](https://m1.examhoop.com/wp-content/ql-cache/quicklatex.com-0db13e82763315022e50a26f7489f4ea_l3.png)